Week 03 Lecture: Neural Network Architectures
Contents
Week 03 Lecture: Neural Network Architectures¶
In the lecture we will survey the following types of neural networks:
Convolutional Neural Networks
Graph Neural Networks
Recurrent Neural Networks
Attention and Transformers
Convolutional Neural Networks¶
Convolutional networks were initialy motivated by image processing tasks (2D data x 3 colors).

Convolutional networks operate on multi-dimensional data by applying filters that are scanned over the data by focusing on data proximity.
The filters are small matrices that capture local features. The small size of the filters also has practical advantages (less memory, easier training).
Convolutional layers encode multi-dimensional data. Fully connected linear layers may be used to ‘read out’ desired classifiers or values.

The convolution operation involves the dot product between the weight matrix calculated by sliding over the input data with the results accumulated across all input layers.
Input data may be padded with zeros. The stride determines how much the weight matrix is advanced at every step. The number of weight matrices determines the depth of the output layer.

Pooling may be used to combine data and reduce the dimensionality.
In most recent networks larger strides are used instead of pooling.

AlexNet is a convolutional network that was very successful ‘early on’ (i.e. 2012) with image classification in the ImageNet Large Scale Visual Recognition Challenge.

ResNet architectures are more advanced convolutional network with additional ‘shortcut’ connections to transfer information between more distant layers.
The main advantage of this architecture is to facilitate the training of very deep networks where vanishing gradients are a common problem. In ResNet models, skipped layers can be excluded initially and added back later to ‘fine-tune’ a model.

Recent networks are even more complicated and can outperform humans in correctly classifiyng objects seen in images.

Convolutional networks can be used for the classification of images in many areas of science, e.g. cryo-electron microscopy images.

Convolutional networks are also well-suited for processing data such as distance matrices.
density grid volumes can be handled via 3D convolutional networks.

multiple sequence alignments are also suitable for convolutional networks after generating a suitable representation of the alignment.
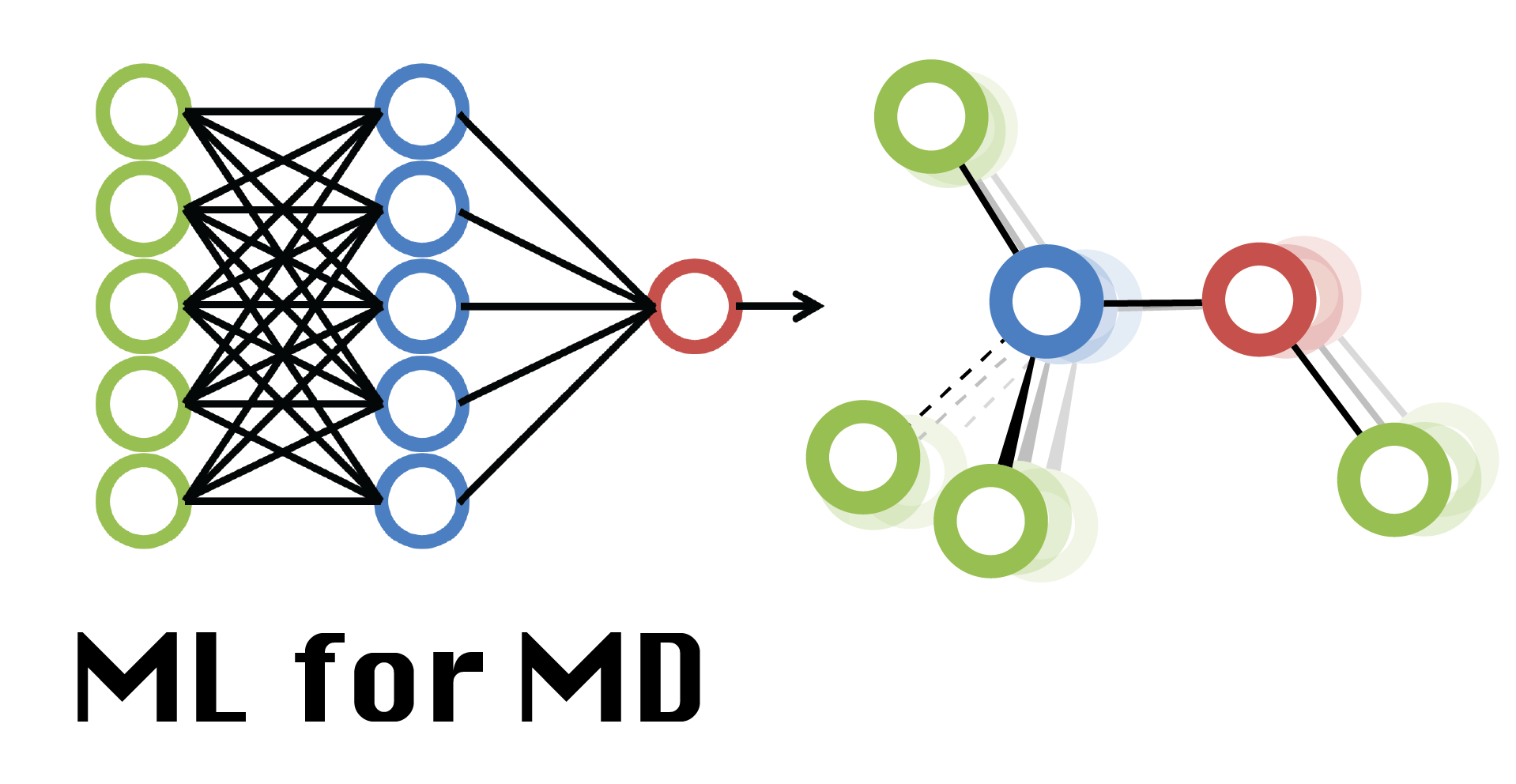
Graph Neural Networks¶

Graph neural networks are designed to capture data that is described by graphs that consist of nodes connected by edges.
Transformations between layers maintain connections and edge properties. Nodes are transformed via convolutions over neighboring nodes. The functions f and g may be represented as fully connected neural networks with trainable weights.
For more information check here.

Graph neural networks are especially relevant for representing molecules:
Nodes: atoms with properties: chemical type, radius, charge, mass, coordinates
Edges: bonds with properties: single/double, covalent, hydrogen-bonding, non-bonded contact
When applied to 3D objects, GNNs should maintain equivariance with respect to translations and rotations. Otherwise, the network model has to learn that translation/rotation does not change objects, training is difficult, and model output is more likely to be non-physical.
For an input layer \(x\) that is transformed to a new layer \(y = \phi(x)\) this requires:
translation equivariance: \( y + T = \phi(x + T) \)
rotational equivariance: \( Ry = \phi(Rx) \)

E(n) Equivariant Graph Neural Networks¶
Satorras, Hoogeboom, Welling: [arXiv: 2102.09844 (2021)] (https://arxiv.org/abs/2102.09844)

Strategies for achieving equivariant transformations typically involve relative distances and radial or spherical harmonic functions.
Other relevant papers on tensor field networks and SE(3) Transformers.
Recurrent Neural Networks¶


Recurrent neural networks focus on capturing sequential processes and were initialy motivated by natural language processing tasks.

Recurrent neural networks involve a hidden state h that is propagated iteratively using the same weight matrix, e.g. with the following non-linear function:
Another recurring weight matrix is used to calculate output values:

In model variations there may be input only at the beginning and at the end.

Or continuous output may be generated iteratively from initial input.
This looks a lot like a conformational sampling algorithm!

A traditional RNN is difficult to train because input at early times affects output much later (vanishing gradients). The LSTM (long short term memory) model provides more control how information is retained over many interations and makes the training of RNNs easier.
Solving Newton’s Equations of Motion with Large Timesteps using Recurrent Neural Networks based Operators¶
Kadupitiya, Fox, Jadhao: arXiv: 2004.06493 (2021)

Recurrent neural networks are well-suited for generating iterative trajectory sampling as in molecular dynamics or Monte Carlo simulations but with longer time steps.
See also recent work from the Tiwary lab.
Transformers¶

Transfomers are more flexible architectures that are replacing RNNs. All of the elements may be a combination of deep (convolutional) network layers.
For structure prediction the ‘input’ may be multiple sequence alignments and the ‘target’ may be an initial template-based model that is subsequently refined via multiple rounds through the decoder.
Attention¶

Transfomers often incorporate attention modules to capture relationships between different elements of sequential data (such as language, sequence data, spatial proximity).